Skip to content
Nombre de Vues : 4 673
Etudier la limite d’une suite ( u n ) , c’est examiner le comportement des termes u n lorsque n prend des valeurs de plus en plus grandes vers + ∞.
Si « u n est aussi grand que l’on veut dès que n est assez grand » , alors on dit que la suite ( u n ) a pour limite + ∞ .
On note lim u n = + ∞
n → +∞
Si les termes u n finissent par être négatifs et « si un est aussi grand que l’on veut en valeur absolue dès que n est assez grand », alors on dit que la suite ( u n) a pour limite – ∞ .
On note : lim u n = – ∞
n → +∞



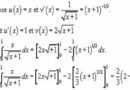 Exercices : Calcul intégrale, intégration par partie
Exercices : Calcul intégrale, intégration par partie 