Exercices corrigés : Dérivées des fonctions exponentielles
La fonction exponentielle est l’unique fonction dérivable sur R qui a pour dérivée elle-même et qui prend la valeur 1 en 0.
cette définition et les premiers résultats qui en découlent peuvent être résumés ainsi :
La fonction exponentielle, notée exp :
– est définie, continue, dérivable et strictement croissante sur R.
– pour tout x : exp’ (x) = exp (x)
– pour tout x : exp (x) > 0
– exp (0) = 1
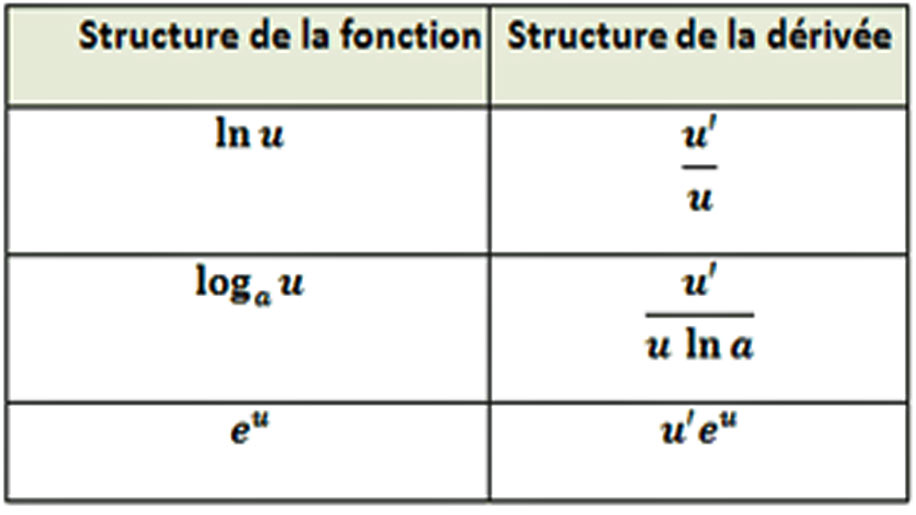
La dérivée de exp(u(x)) est égale à u'(x).exp(u(x)) ( Si u(x) est dérivable) : (exp(u(x))’ = u'(x).exp(u(x).
Le nombre exp(1) étant noté e, (e=2.718)