La notion d’Orthogonalité de deux vecteurs
Definition :
– par convention, le vecteur nul est orthogonal à tout vecteur.
– soient 
et 
deux vecteurs non nuls, et A, B et C trois points tels que
Les vecteurs et sont dits orthogonaux si les droites (AB) et (AC) sont perpendiculaires.
On note :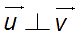 
.
Qui se lit : orthogonal à
Définition du produit scalaire
Definition :
Soient et deux vecteurs de l’espace. – si et sont colinéaires
– si et sont orthogonaux : 
Cas particulier :
Le vecteur nul étant colinéaire et orthogonal à tout vecteur :
More Stories
Exercices résolus sur les équations différentielles
Exercices résolus sur les nombres complexes
Exercices corrigés sur les Primitives et le calcul d’intégrales