Exercices corrigés sur les nombres Complexes ( Terminale générale)
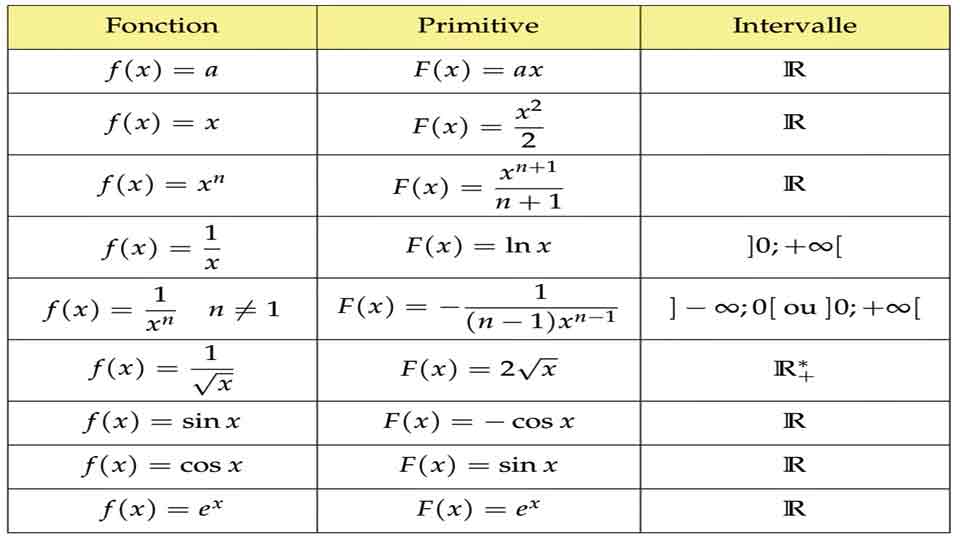
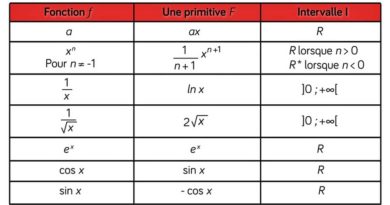
Les nombres complexes : Un nombre complexe est un nombre qui peut s’écrire sous la forme a+bi, où a et b sont des nombres réels et i un nombre imaginaire tel que i²=-1. On peut toujours écrire un nombre complexe z sous la forme : z = |z|(cos(θ)+i sin(θ)), avec θ = arg(z). On appelle ceci la forme trigonométrique de z.
On a : cos(θ) = a.|z| , sin(θ) = b.|z| .
Les nombres complexes vont nous aider à montrer que des droites sont parallèles ou encore que des points sont alignés.
Rappelez-vous toujours que un point M d’affixe z = a + ib peut être placer dans un plan tel que son abscisse soit a et son ordonnée b.
Soient A, B et C trois points du plan d’affixes respectives a, b et c.
Le vecteur vecteur AB a pour affixe (b – a).
La longueur AB vaut le module de l’affixe du vecteur vecteur AB : AB = |b – a|
Les points A, B et C sont alignés si et seulement si les vecteurs et sont colinéaires.
Trois points A, B et C , d’affixes zA, zB et zC, sont alignés si le nombre (zC – zA)/(zB – zA) est réel.
Cette condition exprime que les vecteurs AB et AC sont colinéaires, ce qui se traduit par Arg(AB, AC) = 0.
Exercices sur les nombres Complexes :
Solution des exercices sur les nombres complexes: