En mathématiques, l’ensemble des nombres complexes est créé comme extension de l’ensemble des nombres réels, contenant en particulier un nombre imaginaire noté i tel que i2 = −1. Le carré de (−i) est aussi égal à −1 : (−i)2 = −1.
Tout nombre complexe peut s’écrire sous la forme a + i b où a et b sont des nombres réels.
L’addition et la multiplication des réels s’étendent aux nombres complexes sans difficulté particulière.
-
addition :
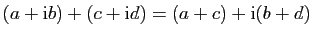 ,
, -
multiplication :
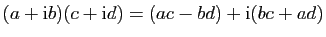 .
.


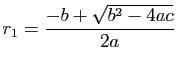 et
et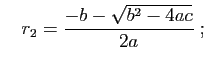
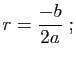
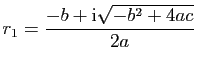 et
et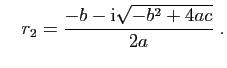




More Stories
Exercices résolus sur les équations différentielles
Exercices corrigés : écriture exponentielle des nombres complexes ( TSTi2D)
Exercices corrigés : Calcul des dérivées ( TSTI2D)