Exercices : Etude de la fonction logarithme Népérien

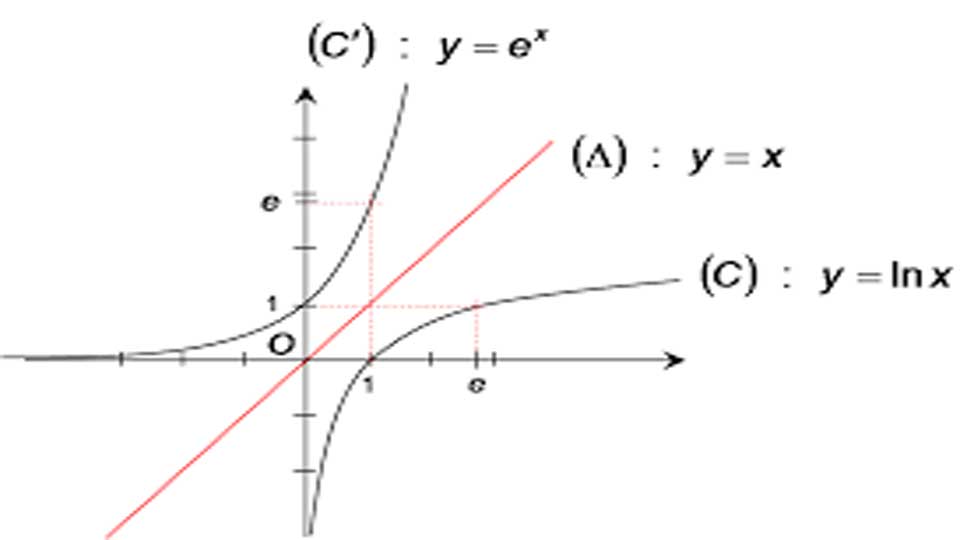
• La fonction logarithme naturel est définie et dérivable (donc continue) sur ]0, +∞[ et pour tout réel x strictement positif,

  

• Puisque cette dérivée est strictement positive, le logarithme naturel est strictement croissant.

• Puisque cette dérivée est strictement décroissante, le logarithme naturel est strictement concave.

• Les limites de la fonction aux bornes de son intervalle de définition sont :

  

  C’est donc une bijection de ]0, +∞[ sur ℝ.

Exercices : 

Correction :