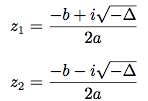
Les nombres complexes : Calcul du module et argument et équations de second degré
Rappel sur les nombres complexes :
Résolutions d’équation du second degré dans l’ensemble des complexes
Soit az² + bz + c = 0 une équation du second degré à coefficient réel, avec a,b,c ∈ 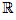 et a ≠ 0.
et a ≠ 0.
Soit Δ = b² – 4ac le discriminant de cette équation. :
-
-
-
Si Δ > 0, alors l’équation admet deux solutions distinctes réelles :
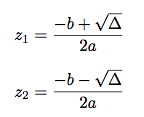
-
Si Δ = 0, alors l’équation admet une unique solution réelle :
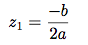
-
Si Δ < 0, alors l’équation admet deux solutions distinctes complexes
-